Brief Overview
Black box optimization focuses on optimizing unknown functions in high-dimensional spaces. In certain applications, evaluating these functions is expensive, hence the optimization must be performed under tight sample budgets. Past works have approached black-box optimization using Gaussian Process Regression (GPR) and sample efficiency has been improved by utilizing information about the shape/structure of the function. We propose to discover the structure of the function by learning a GPR kernel. Learning the kernel is achieved via an auxiliary optimization in (latent) kernel space, realized inside a variation autoencoder. The optimal kernel is expected to best ``explain'' the unknown function, helping lower the sample budget. Results show that our method, Kernel Optimized Blackbox Optimization (KOBO), effectively minimizes the black-box function at a substantively lower sample budget. Results hold not only in synthetic black box functions but also in real-world applications, where audio/images need to be personalized with limited user queries.
Many problems involve the optimization of an unknown objective function. Examples include personalizing content \(x\) to maximize a user's satisfaction \(f(x)\), or training deep learning models with hyperparameters \(x\) to maximize their performance \(f(x)\). Function \(f(x)\) is unknown in these cases because it is embedded inside the human brain (for personalization) or too complex to derive (for hyper-parameter tuning). However, for any chosen sample \(x_i\), the value of \(f(x_i)\) can be evaluated. For hearing-aid personalization, say, evaluating the function would entail playing audio with some hearing-compensation filter \(x_i\) and obtaining the user's satisfaction score \(f(x_i)\). Bayesian methods like Gaussian Process Regression (GPR) are de facto approaches to black-box optimization. Using the set of function evaluations, conventional GPR learns a probabilistic surrogate model \(\hat{f}(x)\) for \(f(x)\). The optimum is estimated on this surrogate as \(\hat{x}^*\) that minimizes \(-\hat{f}(x)\).
\[\text{argmin}_{\hat{x} \in \mathcal{H}} \quad ||f(\hat{x})-f(x^*)||_2\]
\[\textrm{s.t.} \quad Q \leq B\]
where, \(Q\) is the number of times the objective function is evaluated/queried, and the query budget \(B \ll N\). Function \(f\) may be non-convex, may not have a closed-form expression, and its gradient is unavailable.
In most BBO problems, \(f(x)\) is expensive to evaluate, hence a strict sample or query budget \(B\) is of interest.
Techniques that lower this budget have garnered recent attention.
One idea is to exploit domain knowledge about the rough shape of \(f(x)\), i.e., select a GPR kernel that models this shape.
With humans, for example, \(f(x)\) may have a staircase structure as they may not perceive differences in certain neighborhoods of \(x\), but their ratings may change just outside that neighborhood.
If GPR's surrogate model \(\hat{f}(x)\) captures this staircase structure in its kernel, sample efficiency can improve.
The question is, in the absence of domain knowledge,
Our contribution is a kernel learning technique that first creates a continuous space of kernels, then optimizes on that kernel space to find the optimal kernel \(\mathbf{K}^*\) for \(\hat{f}(x)\). Briefly, a Kernel Combiner generates composite kernels by adding or multiplying simple ``basis'' kernels like Radial Basis Function (RBF), Periodic (PE), Matern (MA), etc. The resulting kernel space is discrete as it is composed of discrete kernel choices. Searching this discrete kernel space to obtain the best-suited kernel is difficult, hence we propose a generative model -- a Kernel Space Variational Autoencoder (KerVAE) -- that learns a low-dimensional continuous manifold of the discrete kernels. This manifold lives in the latent space of the VAE and computing the effectiveness of each kernel is also a black box function because it is prohibitively expensive. Hence, kernel learning is achieved through a Kernel Space GPR (KerGPR) that optimizes this low-dimensional manifold to find \(\mathbf{K}^*\).
KOBO: Kernel Optimized BO
Figure above shows the complete Kernel Optimized Blackbox Optimization KOBO model, with two main modules:
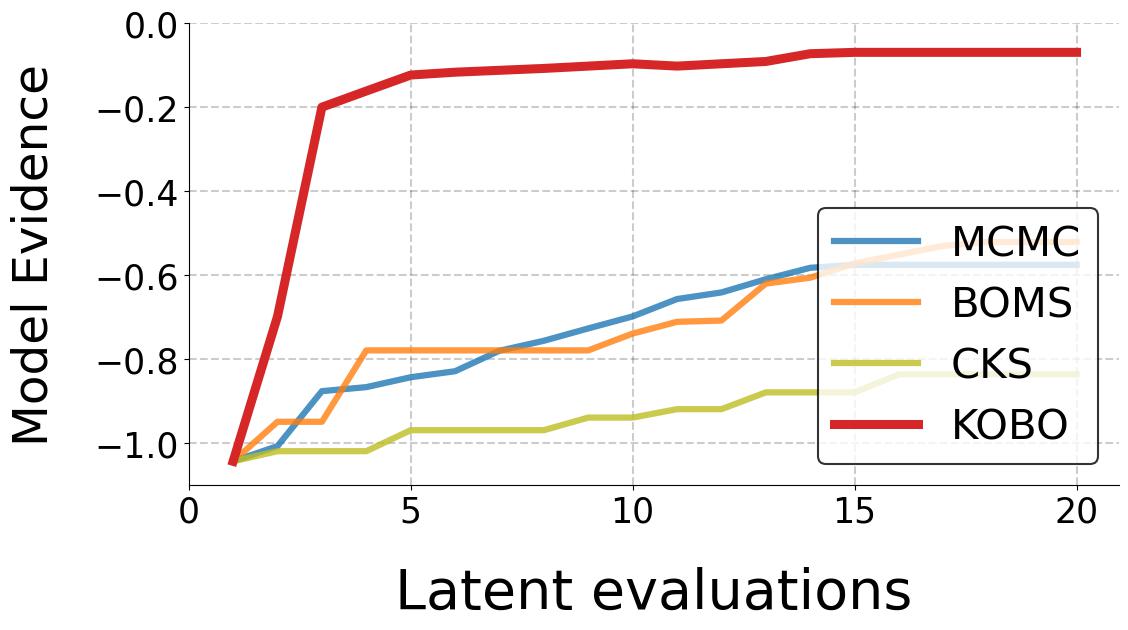
- Function GPR (\(f\)GPR}) - This is a Bayesian framework aimed at optimizing the objective function \(f(x)\) through a GPR that uses an initial kernel to generate surrogate functions, and then uses an acquisition function to decide the next sample \(x_i\) to evaluate. This module forwards the model evidence, \(p(\mathcal{F} | \mathcal{X}, \mathbf{K})\) to the second module and receives updated kernel prescriptions from it.
- Kernel Learning - This second module learns the continuous kernel space through a kerVAE and applies a GPR on the latent space to estimate \(z^*\). The GPR uses model evidence for the optimization, and returns the optimal kernel \(\mathbf{K}^*\) to \(f\)GPR. The iterations occur until the query budget \(B\) has been expended.
Synthetic Function Results
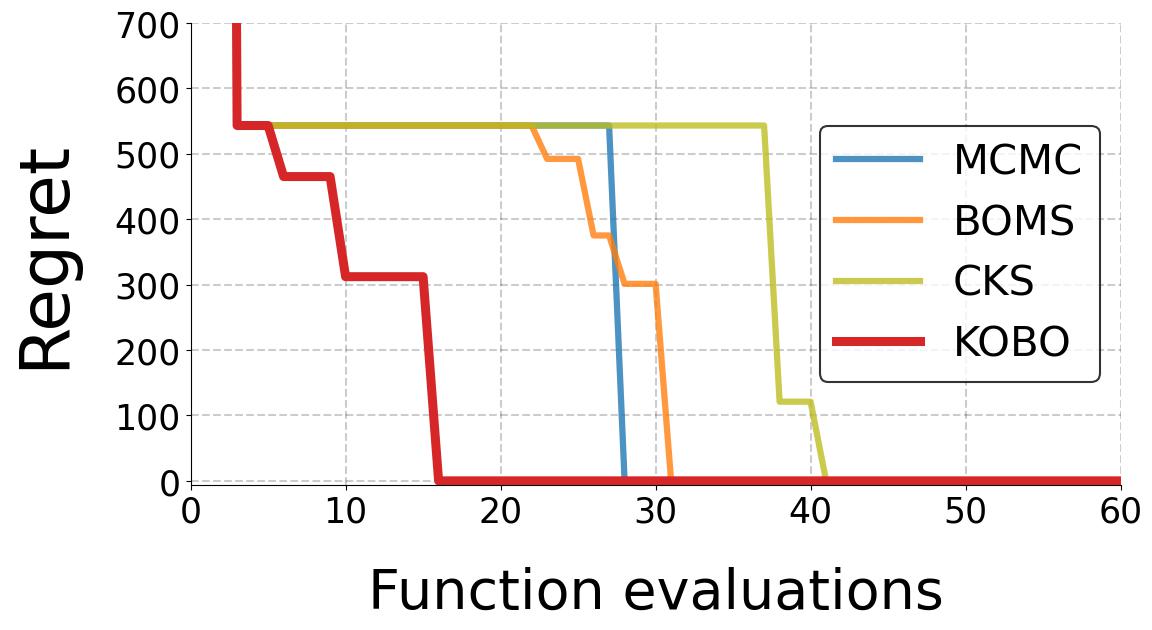
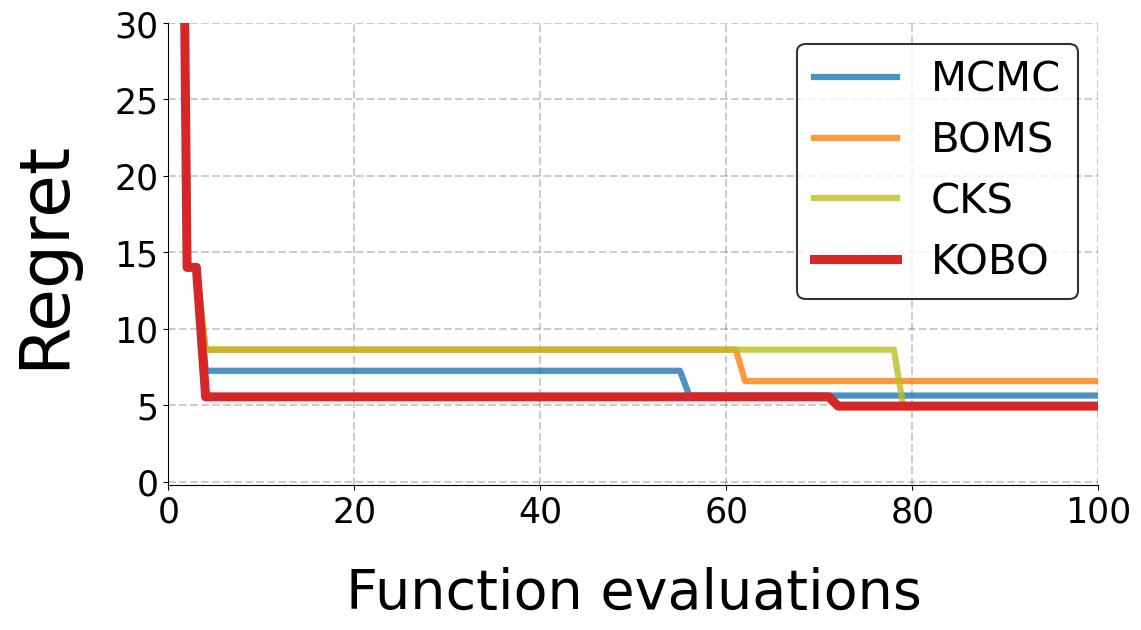
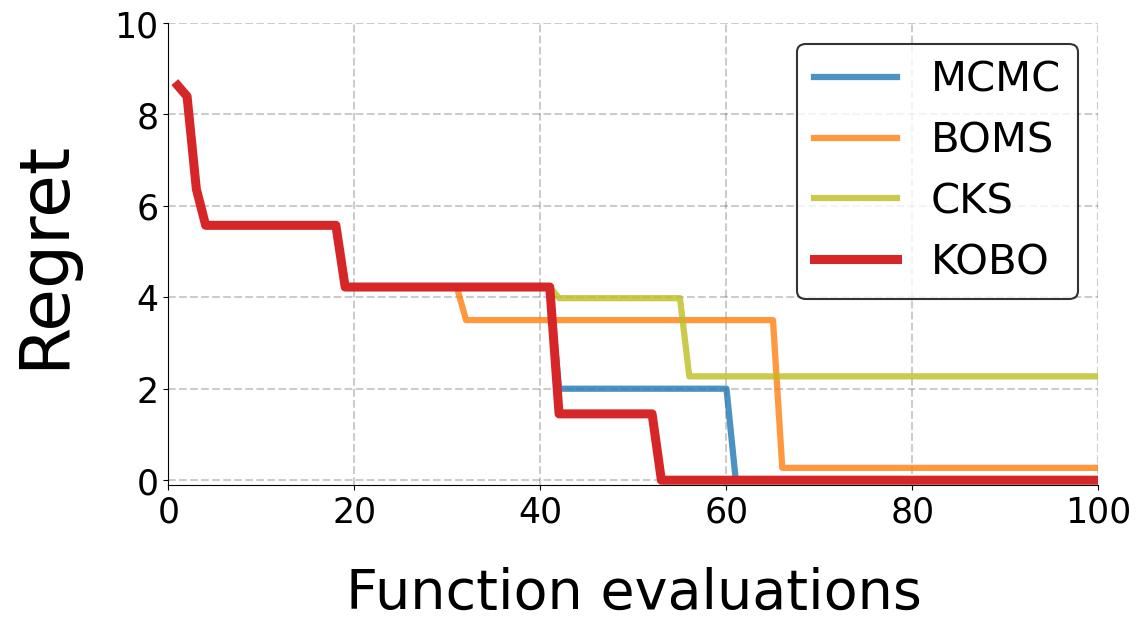
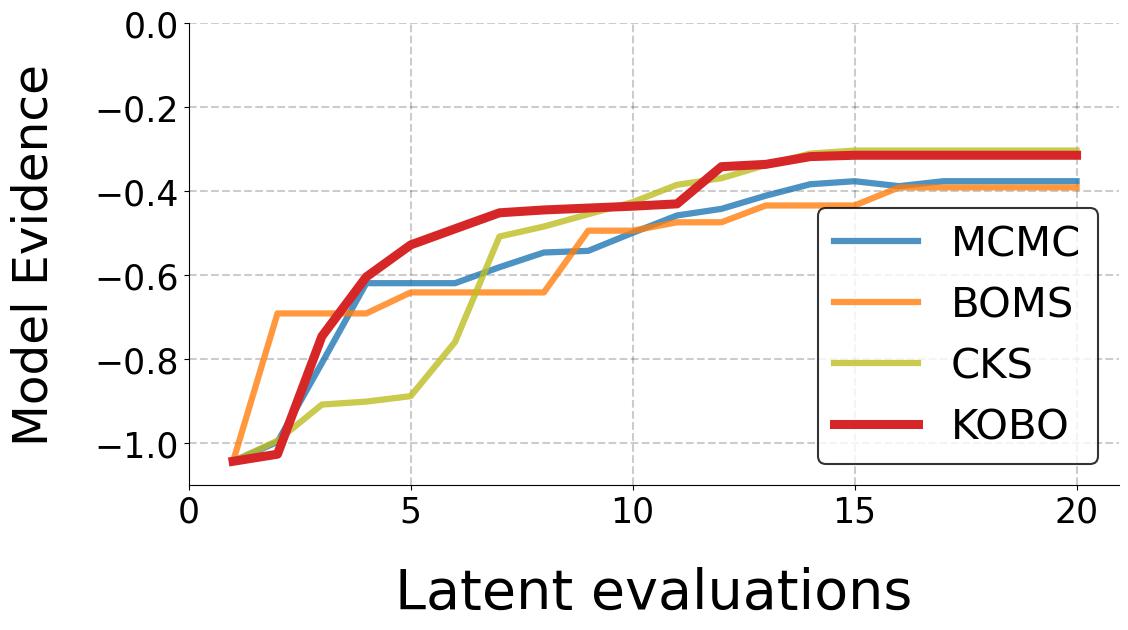
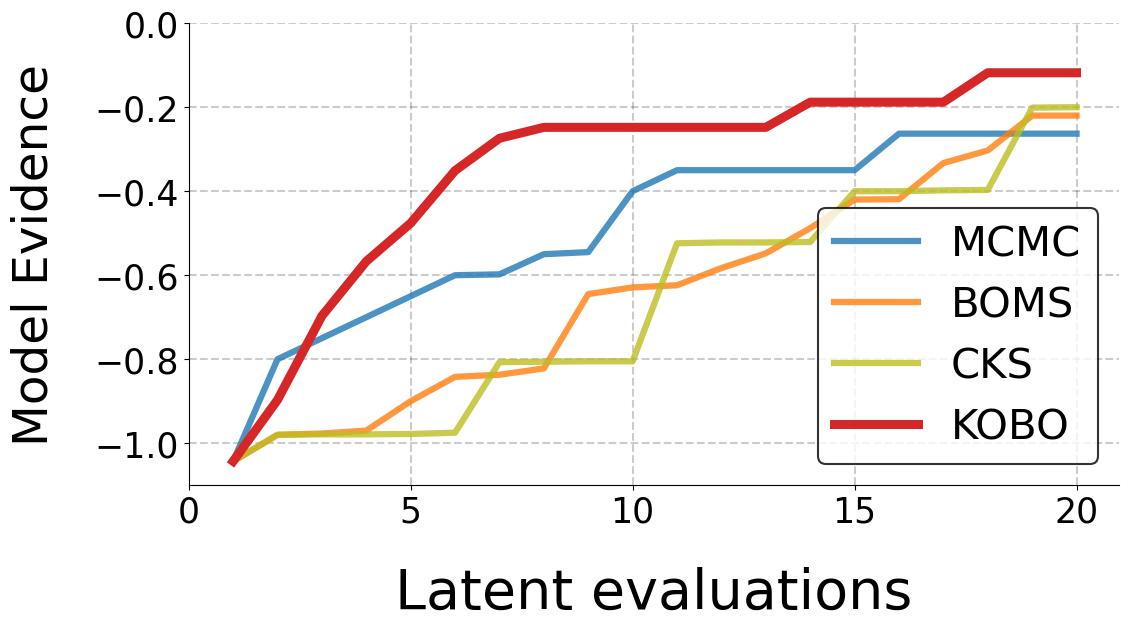
We intend to characterize the performance of KOBO for synthetic satisfaction functions (with a staircase shape as shown in the Figure above) We compare with a baseline as follows:
- MCMC [1] - MCMC-based kernel learning method that uses Metroplis-Hastings algorithm to sample kernel space to obtain the optimal kernel \(\mathbf{K}^*\) that maximizes Model Evidence.
- KOBO - Our proposed algorithm that optimizes a continuous learned kernel latent space to determine the optimal kernel \(\mathbf{K}^*\) that matches the function \(f(x)\) thereby reducing the queries.
Results below show that KOBO outperforms MCMC and achieves the minimum \(\hat{f}_{min}\) much quicker.
Audio Personalization Demo and Results
Corruption
We inject two types of corruption to the Ground Truth audio:
- We corrupt each frequency of the audio clip using a hearing loss profile from a publicly available dataset [2].
- We corrupt using a random filter which distorts each frequency independently within [-30,30] dB, i.e., \(h_r[j] \in [-30,30]{dB}, j=0,1,\dots,N\).
KOBO
KOBO plays audio clips that are filtered with different carefully designed filters (\(x_i\)), and the user gives scores for these clips. After every batch of 5 user queries, KOBO updates the \(f\)GPR kernel with the optimal \(\mathbf{K}^*\) obtained by KerGPR. Observe that this can even be done on the fly as the user listens to music or watches the news.
Baselines - SE, PER
Our baselines are conventional GPR with SE kernel and PER kernel and do not learn a optimal kernel.
Audio Demos
The audio demo below has 2 tables: (1) the hearing loss corruption case, and (2) the random corruption case. The table columns are example audio clips heard by six different users (U1-U6). The table rows indicate the number of queries \(Q\) used. The following are the different types of audio clips generated:
- Ground Truth: The original audio clip
- Corrupted: The audio clip after applying the corruption (hearing loss or random) filter.
- SE: The audio clip after applying conventional GPR with SE kernel (from querying the user \(Q\) times).
- PER: The audio clip after applying conventional GPR with PER kernel (from querying the user \(Q\) times).
- KOBO: The audio clip after applying the personal filter generated by KOBO (from querying the user \(Q\) times).
*Note: The audio quality you hear in the following
demos will be influenced by the frequency response of your audio-speaker, hence the quality you experience will not accurately reflect the quality perceived by users U1, U2, U3.
KOBO is actually compensating for each user’s audio-speaker’s response function as well, hence users U1, U2, U3, U4, U5, U6 should have
heard a better quality.
The Hearing Loss Corruption case
| Ground Truth | Corrupted | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Query | User 1 | User 2 | User 3 | User 4 | User 5 | User 6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | |
| \(Q=5\) | ||||||||||||||||||
| \(Q=10\) | ||||||||||||||||||
| \(Q=15\) | ||||||||||||||||||
| \(Q=20\) | ||||||||||||||||||
| \(Q=25\) | ||||||||||||||||||
The Random Corruption case
| Ground Truth | Corrupted | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Query | User 1 | User 2 | User 3 | User 4 | User 5 | User 6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | SE | PER | KOBO | |
| \(Q=5\) | ||||||||||||||||||
| \(Q=10\) | ||||||||||||||||||
| \(Q=15\) | ||||||||||||||||||
| \(Q=20\) | ||||||||||||||||||
| \(Q=25\) | ||||||||||||||||||
User Satisfaction Score Results
The table below shows the User Satisfaction Scores for (a) Hearing Loss and (b) Random filters corresponding to the Audio clips above.
Rebuttal
Additional Results
Comparison of KOBO with other kernel learning methods
We compare KOBO to the following kernel learning methods:
- MCMC [1] - MCMC-based kernel learning method that uses Metroplis-Hastings algorithm to sample kernel space to obtain the optimal kernel \(\mathbf{K}^*\) that maximizes Model Evidence.
- CKS [3] - CKS is a greedy search algorithm. CKS generates complex kernels as compositions of base kernels through addition and multiplication. It treats the kernel selection as a tree search over the discrete kernel space \(\mathcal{K}\). Model Evidence is the metric that informs the next composite kernel generated at each node traversal.
- BOMS [4] - BOMS uses Bayesian Optimization to find the optimal kernel \(\mathbf{K}^*\) in discrete kernel space \(\mathcal{K}\). To navigate the BO search in the discrete space, BOMS defines a kernel similarity measure called "Hellinger Distance". This distance is used to compute the covariance of the Gaussian distribution of the BO. This “kernel-kernel” is needed to move from one kernel to another during the search. Kernels which are a certain Hellinger distance away from base kernels form the “active model set” on which BO is applied.
Results below (Updated Figure 6 in paper) show that KOBO outperforms MCMC, CKS, and BOMS. KOBO achieves the minimum \(\hat{f}_{min}\) much quicker.
KOBO presents an efficient search of the discrete kernel space \(\mathcal{K}\). The continuous latent space learned by KerVAE simplifies the KerGPR optimization to determine \(\mathbf{K}^*\). This outperforms sub-optimal strategies like greedy search (CKS) and heuristic metrics for BO in discrete space (BOMS).
Ablation Study: Effect of grammar-based kernel encoding \(r_c\) length \(L\)
In the paper we used encodings of length \(L=15\). We compare two additional lengths \(L=5\) and \(L=25\):
Results below (Updated Figure 6 in paper) show that the encoding length \(L\) has diminishing advantage.
For the staircase objective function, we observe that a larger encoding length \(L=25\) does not offer significant gains over the chosen legth \(L=15\). However, length \(L=5\) is not enough to generate kernels with enough complexity to model the objective function structure. Thus, \(L=15\) is a good choice for the function considered.
References
[1] Gardner, Jacob, et al. "Discovering and exploiting additive structure for Bayesian optimization." Artificial Intelligence and Statistics. PMLR, 2017.
[2] NHANES CDC. 2011. Centers for Disease Control and Prevention (CDC). National Center for Health Statistics (NCHS). National Health and Nutrition Examination Survey Data, Hyattsville, MD
[3] D. Duvenaud, J. R. Lloyd, R. Grosse, J. B. Tenenbaum, and Z. Ghahramani. "Structure Discovery in Nonparametric Regression through Compositional Kernel Search". In International Conference on Machine Learning (ICML), 2013.
[4] M. Gustavo, C. Schaff, and R. Garnett. "Bayesian optimization for automated model selection." Advances in neural information processing systems 29 (2016).